题目简介

1601. 最多可达成的换楼请求数目

难度：困难

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests ，其中 requests[i] = [fromi, toi] ，表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。

一开始所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

示例1：

2.png

1
2
3
4
5
6
7
8
9
10
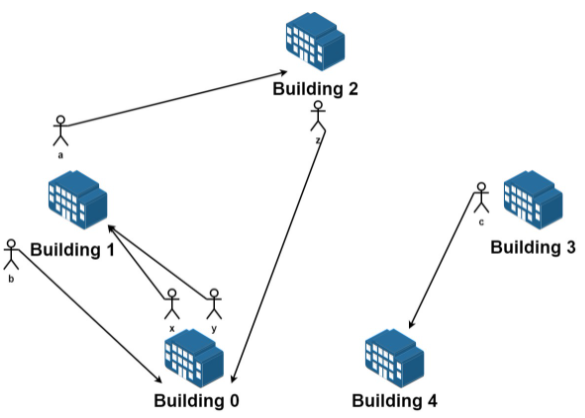
11
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

示例2：

1
2
3
4
5
6
7
输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

解法

时间与内存情况：

1.png

首先设requests的长度为 m。

本题数据范围很小，n的范围为 20，m 的范围为 16。

所以可以使用穷举法。但需要进行状态压缩。

我们可以使用一个二进制数state表示当前状态，如果二进制数的第i位为1，则表示requests[i]被选择。这样的话一共有2的m次方种状态。

枚举所有状态，如果当前状态中二进制位的1数量小于等于res值，那么直接continue就可以，无需检查合法性。大于res则检查合法性，合法则赋值给res，最后返回res即可。

代码中bits.OnesCount作用为检查一个uint数字中包含有多少个1，(s >> i) & 1用于判断s的第i位是不是1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func maximumRequests(n int, requests [][]int) int {
    states_sum := 1 << len(requests)
    res := 0
    for state := 0; state < states_sum; state++ {
        num := bits.OnesCount(uint(state))
        if num <= res {
            continue
        } else if check(state, requests) {
            res = num
        } else {
            continue
        }
    }
    return res
}

func check(s int, rq [][]int) bool {
    balance := [20]int{}
    for i := 0; i < 20; i++ {
        if (s >> i) & 1 == 1 {
            balance[rq[i][0]]--
            balance[rq[i][1]]++
        }
    }
    for _, b := range balance {
        if b != 0 {
            return false
        }
    }
    return true
}